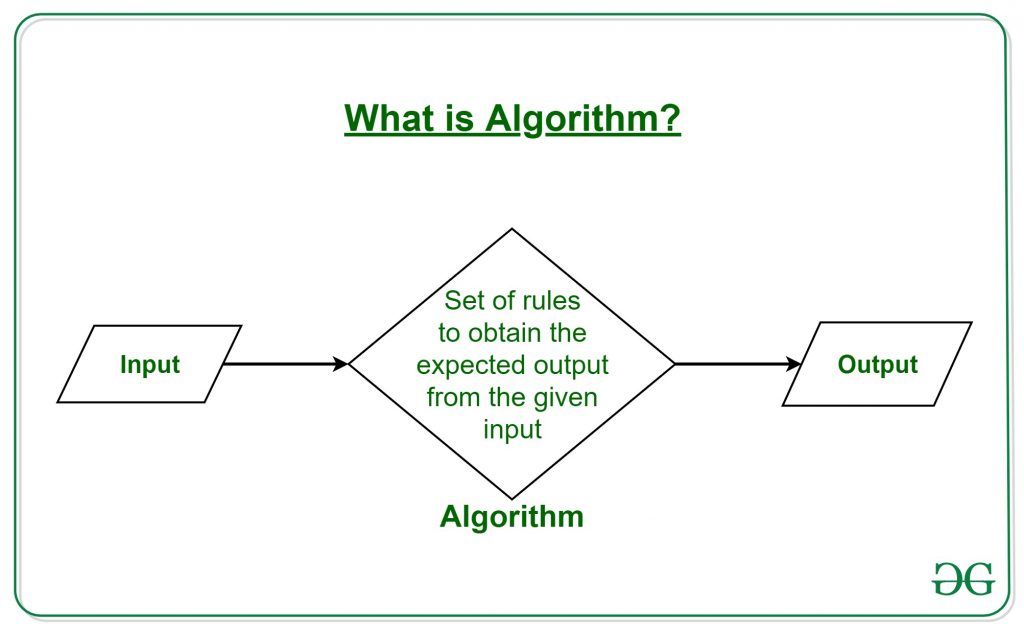
What is an algorithm? It's a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation (Wikipedia).

A representation of an algorithm. Source: GeeksForGeeks.

Let's suppose we have an array whose elements are all integers. How do we know if any of those integers is the number 50?

We can feed this array to an algorithm that will return a boolean as an answer.

 It's pseudocode could be expressed like this:

For i from 0 to n-1
    If 50 is in element[i]
        Return true
Return false

This is an instance of a search algorithm, that is, one "which solves the search problem, namely, to retrieve information stored within some data structure, or calculated in the search space of a problem domain, either with discrete or continuous values." (Wikipedia).

In particular, our example would be a type of search algorithm called linear search: one that "starts at one end and goes through each element of a list until the desired element is found, otherwise the search continues till the end of the data set." (GeeksForGeeks).

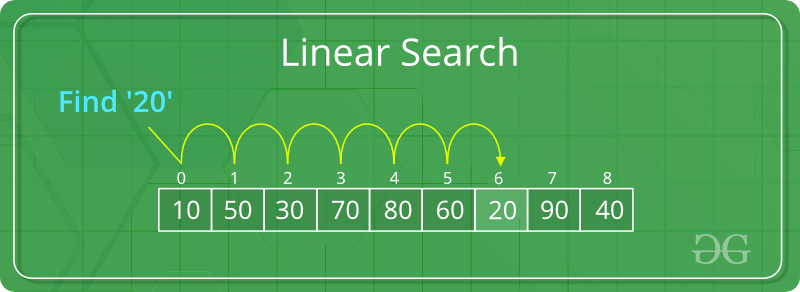
A representation of a linear search algorithm (Source: GeeksForGeeks).

Another more efficient search algorithm for solving our problem is binary search. If our array fulfills the requirement that its elements are already ordered, this algorithm works by using that information by repeatedly dividing the search space in half. 
Its pseudocode could be like this:

Repeat until finding 50 or exhausting items:

    Divide array in left and right half by finding item[middle]
        If item[middle] is = 50
            Return true
    Else if item[middle] > 50
        Search through left half(from first to middle -1)
    Else if item[middle] < 50
        Search through right half(from middle +1 to n-1)

So let's suppose we have an ordered array of n = 120, and we want to find out if 50 is among the items in that array. These would be the steps following binary search:
 

array n = 120
i want to find out if the array includes the number 50

divide search space: left(from 0 to 59) and right(from 61 to 120)
middle is 60
is middle = 50 ? NO
is middle > 50 ? YES
browse left half of search space: from 0 to 59

divide search space: left(from 0 to 29) and right(from 31 to 59)
middle = 30
is middle = 50 ? NO
is middle > 50 ? NO
is middle < 50 ? YES
browse right half of search space: from 31 to 59

divide search space: left(from 31 to 44) and right (from 46 to 59)
middle = 45
is middle = 50 ? NO
is middle > 50 ? NO
is middle < 50 = YES
browse right half of search space: from 46 to 59

divide search space: left(from 46 to 51) and right (from 53 to 59)
middle = 52
is middle = 50 ? NO
is middle > 50 ? YES
browse left half of search space: from 46 to 51

divide search space: left(46 to 47) and right (from 49 to 51)
middle = 48
is middle = 50 ? NO
is middle > 50 ? NO
is middle < 50 ? YES
browse left half of search space: from 49 to 51

divide search space: left(49) and right (51)
middle = 50
is middle = 50 ? YES
Return true !!!

As you can see, using this search algorithm would be more efficient as it would cost less running time than linear search. 

As mentioned here, “binary search is well-suited for searching large datasets that are stored in external memory, such as on a hard drive or in the cloud.”

To analyze and compare the efficiency of search (and other types of) algorithms and, more precisely, to understand how their performance scales with increasing input sizes, Big O notation is used. This is a mathematical notation used in computer science to describe the performance or complexity of an algorithm, and the time it would take to run it regardless of other variables like hardware.

As explained here, "efficiency is measured in two ways: time complexity and space complexity. A function's time complexity measures how long it takes to execute in terms of computational steps. The space complexity of a function is determined by the amount of memory it uses."

Big O notation is written as O(f(n)), where "f(n)" represents the upper bound of the algorithm's growth rate concerning the input size "n."

Scientists refer to the efficiency and scalability of algorithms in terms of the order of various running times. For instance, we refer to the first [O(n)] as “in the order of n”.

Big O notation simplifies the analysis by focusing on the dominant term that grows the fastest as the input size increases. Constants and lower-order terms are often ignored because they have a lesser impact on the overall growth rate. Therefore, it describes the worst-case scenario. It provides an upper limit on the running time or space usage, ensuring that the algorithm will not perform worse than the stated complexity.

For instance, as explained here, “if an algorithm has the number of operations required formula of:

f(n) = 6n^4 - 2n^3 + 5

As “n” approaches infinity (for very large sets of data), of the three terms present, 6n^4 is the only one that matters. So the lesser terms, 2n^3 and 5, are actually just omitted because they are insignificant. Same goes for the “6” in 6n^4, actually. Therefore, this function would have an order growth rate, or a “big O” rating, of O(n^4).”

You can see various common running times in the following graph. Notice that it’s the shape of the curve that shows the efficiency of an algorithm:

Representation of various running times using Big O notation, from more efficient (in green) to less efficient (in red). Source: Reducible Youtube channel. 

We can explain some of them:

O(1) – Constant time: the fastest one. This means that the runtime will always be the same regardless of the input size. For instance, an algorithm for returning the first element of an array.

O(n) – Linear time: When the running time of an algorithm increases linearly with the size of the input. For instance, linear search. Another example (as explained here) would be any function that implements a simple loop, e.g., an algorithm that returns the factorial of any inputted number. This means if you input 5 then you are to loop through and multiply 1 by 2 by 3 by 4 and by 5 and then output 120.

O(log n) – Logarithmic time: this is similar to linear time, except that its runtime does not depend on the input size but rather on half the input size. That is to say that the input size decreases on each iteration or step. Binary search is an example of this, as it reduces the search space by half in each step.

We will review other algorithmic complexities in a following blog post, when we talk about sorting algorithms.